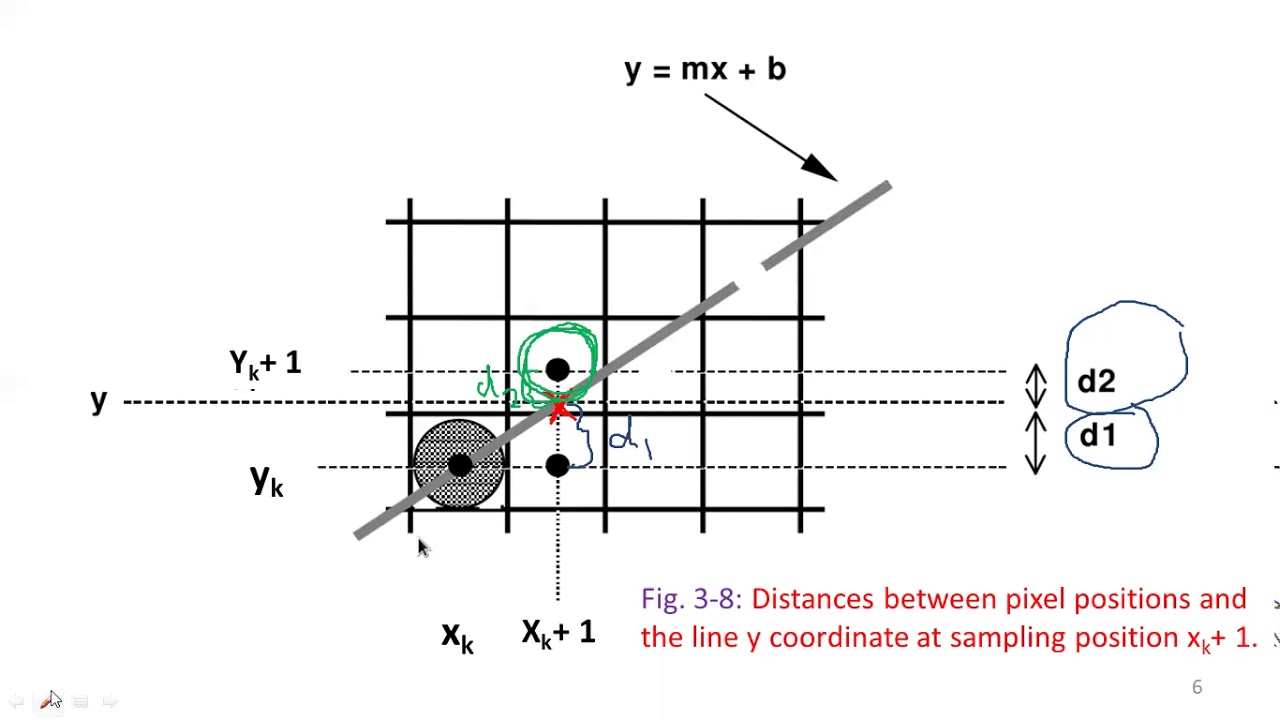
Consider line segment where m is between -1 and +1.
In order to determine pixels, we move along the x-direction in unit steps from the current position (x_k,y_k).
At each of these steps, we have to choose between the two y values y_k and y_(k+1).
Clearly, we would like to choose a pixel that is closer to the original line. Our choices of pixels are (x_(k+1),y_1) or (x_(k+1),y_(k+1)).
Denote:
d_upper=(y_k+1)-y
d_lower=y-y_k
We know
y=mx+b is the equation of a line.
Now we calculate the difference between d_lower and d_upper.
d_lower-d_upper
= mx_k+m+b-y_k-y_k-1+mx_k+m+b
=2m(x_k+1)-2y_k+2b-1
Substitute m with dy/dx.
d_lower-d_upper=2dy/dx*(x_k+1)-2y_k+2b-1
dx(d_lower-d_upper)=2dyx_k-2dxy_k+2dy+dx(2b-1)
= 2dyx_k-2dxy_k+c
Where c=2dy+dx(2b-1)
Let us denote dx(d_lower-d_upper) by p_k, a decision parameter for the kth step.
At step k+1, the decision parameter is
p_(k+1)=2dyx_(k+1)-2dxy_(k+1)+c
Subtracting p_k from p_(k+1), then substituting x_(k+1)=x_k+1 and rearranging we get
p_(k+1)=p_k+2dy-2dx(y_(k+1)-y_k)
After this the author writes that the first decision parameter p_0=2dy-dx. However he doesn’t provide much explanation for it.
Can anyone help me derive the initial parameter?